华南师范大学附属中学罗碎海解答数学B卷答案及简略解答

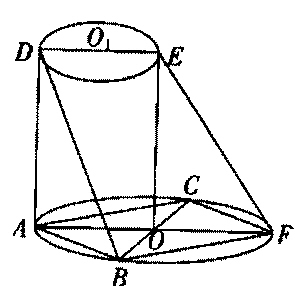
　　15.f(x)=sinx+sin(x+■）=sinx+cosx=■sin(x+■)

　　（Ⅰ）f(x)=sinx+sin(x+■)，x∈R是周期函数，最小正周期为2。

　　（Ⅱ）f(x)的最大值为■，最小值为-■ （Ⅲ）∵f()=■，∴sin+cos=■

　　∴sin2=2sincos=(sin+cos)2-1=■-1=-■。

　　16.（Ⅰ）该运动员两次都命中7环的概率为p=0.2×0.2=0.04 （Ⅱ） 的取值：0~6，7.8.9.10

　　p(=k)=p(一次命中k环，另一次小于k环)+{两次都k环}

　　成绩分布图

　　0~6

　　7

　　8

　　9

　　10

　　0~6

　　7

　　7

　　8

　　9

　　10

　　10

　　10

　　10

　　10

　　10

　　8

　　8

　　8

　　9

　　10

　　9

　　9

　　9

　　9

　　10

　　p(=0~6）=0

　　p(=7）=0.2×0.2=0.04

　　p(=8）=2×0.3×0.2+0.32=0.21

　　p(=9）=2×0.3×(0.2+0.3)+0.32=0.39

　　p(=10）=2×0.2×(0.2+0.3+0.3)+0.22=0.36

　　故∫的分布列

　　p

　　0~6

　　0

　　7

　　0.04

　　8

　　0.21

　　9

　　0.39

　　10

　　0.36

　　（Ⅲ）E=7×0.04+8×0.21+9×0.39+10×0.36=9.07 答：的数学期望为9．07

　　17．（Ⅰ）∵AD⊥平面ABF AB·AF平面ABF，二者推出∴AD⊥AB、AD⊥AF ∴∠BAF就是二面角B－AD－F的平面角。又∵AF·BC是⊙0的直径，AB＝AC＝6，二者推出ABFC是正方形，推出∠BAF＝45°

　　（Ⅱ）连DO，由已知DE＝A0＝OF，∴ODEF为平行四边形。∠ODB为两弄面线BD与EF所成角，又由（Ⅰ）知 ABFC是边长为6的正方形推出BC⊥AF，AD⊥平面ABF，∴AO是OD在平面ABF上的射影。由三垂线定理知OD⊥BC，由AB＝AC＝6推出OB＝3■，AB＝6、AD＝8推出DB＝10，∴sin∠ODB=■=■，∴直线BD与EF所成角为arcsin■